
概念
定义
由 $m \times n$ 个数排成m行n列的数表
$$
\begin{bmatrix}
a_{11} & a_{12} & … & a_{1n} \
a_{21} & a_{22} & … & a_{2n} \
… & … & … & … \
a_{m1} & a_{m2} & … & a_{mn} \
\end{bmatrix}
$$
称为一个 $m \times n$ 矩阵。其中$a_{ij}$称为矩阵的第i行第j列元素
表示:$A$或$A_{m \times n}$
当$m = n$时, $A_{n \times n}$ 称为n阶方阵或n阶矩阵,也记为$A_n$
元素是实(复)数的矩阵称为实(复)矩阵
同型矩阵与矩阵相等
同型矩阵
两个矩阵行数相等,列数也相等
矩阵相等
设$A=(a_{ij})$与$B=(b_{ij})$为同型矩阵,且对应元素也相等,则称矩阵A与B相等,记做$A=B$
几种特殊的矩阵
零矩阵
元素全为0的矩阵称为0矩阵,$m \times n$ 零矩阵记做$O_{m \times n}$, 或 $O$
单位矩阵
主对角线元素全为1,其余元素全为零的方阵称为单位矩阵,记为$E$或$I$
$$
E = E_n =
\begin{bmatrix}
1 & 0 & … & 0 \
0 & 1 & … & 0 \
… & … & … & … \
0 & 0 & … & 1
\end{bmatrix}
$$
行矩阵与列矩阵
仅有1行的 $1 \times n$ 矩阵 $a=|a_1, a_2, …, a_n|$ 称为一个行矩阵或n维行向量,$a_i$称为向量a的第i个分量
仅有一行的列 $m \times 1$矩阵称为一个列矩阵或m维列向量
上三角矩阵与下三角矩阵
主对角线下边的元素全为零的n阶方阵称为上三角矩阵
$$
\begin{bmatrix}
a_{11} & a_{12} & … & a_{1n} \
0 & a_{22} & … & a_{2n} \
… & … & … & … \
0 & 0 & … & a_{nn}
\end{bmatrix}
$$
主对角线上边的元素全为零的n阶方阵称为下三角矩阵
$$
\begin{bmatrix}
a_{11} & 0 & … & 0 \
a_{21} & a_{22} & … & 0 \
… & … & … & … \
a_{n1} & a_{n2} & … & a_{nn}
\end{bmatrix}
$$
对角矩阵
主对角线以外的元素全为零的n阶方阵, 称为n阶对角矩阵
$$
D =
\begin{bmatrix}
d_1 & 0 & … & 0 \
0 & d_2 & … & 0 \
… & … & … & … \
0 & 0 & … & d_n
\end{bmatrix}
$$
记为 $D = diag(d_1, d_2, … , d_n)$
运算
加法及数与矩阵的乘法
加法
设 $A = (a_{ij}){m \times n}$ 和 $B = (b{ij}){m \times n}$ 是两个同型矩阵, 规定 A 与 B的和是由 A 与 B的对应元素相加所得到的的矩阵,记做 $A + B$
$$
A + B =
\begin{bmatrix}
a{11} + b_{11} & a_{12} + b_{12} & … & a_{1n} + b_{1n} \
a_{21} + b_{21} & a_{22} + b_{22} & … & a_{2n} + b_{2n} \
… & … & … & … \
a_{m1} + b_{m1} & a_{m2} + b_{m2} & … & a_{mn} + b_{mn} \
\end{bmatrix}
$$
减法
对于矩阵 $B = (b_{ij}){m \times n}$ ,称 $(- b{ij})_{m \times n}$ 为 B 的负矩阵,记做 - B
减法 $A - B = A + (- B) = (a_{ij} - b_{ij})_{m \times n}$
加法运算规律
- $A + B = B + A$
- $(A + B) + C = A + (B + C)$
- $A + O = A$
- $A + (-A) = O$
数乘
设矩阵 $A = (a_{ij}){m \times n}$ ,k为数,规定k与A的乘积 是用k去乘A的每个元素所得到的的 $m \times n$ 矩阵,记做 $kA$ 或 $Ak$ ,即 $kA = k(a{ij})_{m \times n}$
数乘运算规律
设A、B为 $m \times n$ 矩阵, k、 l为任意常数,则有
- $k(lA) = klA$
- $(k+l)A = kA + lA$
- $k(A + B) = kA + kB$
矩阵相加与数乘矩阵结合起来,统称为矩阵的线性运算
乘法
设 $A=(a_{ij}){m \times n}$,$B=(b{ij}){m \times n}$ 规定A与B的乘积为矩阵 $C=(c{ij})_{m \times n}$, 记为 $AB=C$,其中
$$
C_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j} + … + a_{is}b_{sj} = \sum_{k=1}^{s}a_{ik}b_{kj}
$$
两个矩阵可以相乘的条件:左矩阵的列数=右矩阵的行数
乘法运算规律
- $ABC=A(BC)$
- $\lambda(AB)=(\lambda A)B=A(\lambda B)$
- $A(B+C)=AB + AC$
- $AO=O,OA=O$
- $EA=A, AE+A$
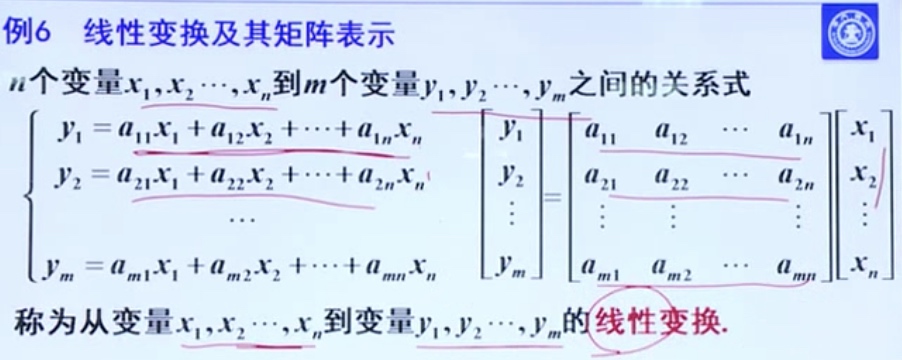
方阵的幂
设A为n阶方阵,定义A的幂为 $A^0=E, A^1=A, A^2=AA, …,A^m=AAAAA…$
由定义,显然 $A^lA^k=A^{l+k}, (A^l)^k = A^{lk}$, 其中l,k为任意非负整数
矩阵的转置
定义
把矩阵$A=(a_{ij})_{m \times n}$ 的行依次换成列(列依次换成行)所得到的 $n \times m$矩阵,称为A的转置矩阵,记为 $A^T$
运算规律
- $(A^T)^T=A$
- $(A+B)^T=A^T+B^T$
- $(kA)^T=kA^T$
- $(AB)^T=B^TA^T$
对称阵与反对称阵
若方阵 $A=(a_{ij}){n \times n}$ 满足 $A^T=A$ ,或 $a{ij}=a_{ji} (i,j=1,2,..,n)$ 则称A为对称矩阵
$$
A=
\begin{bmatrix}
12 & 6 & 1 \
6 & 8 & 0 \
1 & 0 & 6 \
\end{bmatrix}
$$
特点:元素以主对角线为对称,元素对于相等。
若方阵 $B=(b_{ij}){n \times n}$ 满足 $B^T=-B$ ,或 $b{ij}=-b_{ji} (i,j=1,2,..,n)$ 则称B为反对称矩阵,反对称矩阵中
$$
A=
\begin{bmatrix}
0 & -6 & 1 \
6 & 0 & 2 \
-1 & -2 & 0 \
\end{bmatrix}
$$
方阵的行列式
定义
由n阶方阵A的元素所构成的行列式,称为方阵A的行列式,记做$|A|$ 或 $detA$
运算
- $|A^T|=|A|$
- $|\lambda A| = \lambda ^n|A|$
- $|AB|=|A||B|$
逆矩阵
定义
对于n阶方阵A,如果有一个n阶方阵B,使得AB=BA=E,则称方阵A是可逆的,并把方阵B称为A的逆矩阵,A的逆矩阵记做$A^{-1}$
定理
- 若A是可逆矩阵,则A的逆矩阵是唯一的
- 若矩阵A可逆,则$|A|\neq0$
伴随阵
行列式$|A|$的各个元素的代数余子式$A_{ij}$所构成的如下的矩阵
$$
A^*=
\begin{bmatrix}
A_{11} & A_{21} & … & A_{n1} \
A_{12} & A_{22} & … & A_{n2} \
… & … & … & … \
A_{1n} & A_{2n} & … & A_{nn}
\end{bmatrix}
$$
称为矩阵A的伴随矩阵,简称伴随阵
$AA^ = A^A=|A|E$
若$|A|\neq 0$, 则矩阵A可逆,且
$A^{-1}=\frac{1}{|A|}A^*$
逆矩阵的基本性质
若A,B为同阶可逆矩阵,$k \neq 0$,则有
- $A^{-1}可逆,且(A^{-1})^{-1}=A$
- $A^T可逆,且(A^T)^{-1}=(A^{-1})^{T}$
- $kA可逆,且(kA)^{-1}=\frac{1}{k}A^{-1}$
- $AB可逆,且(AB)^{-1}=B^{-1}A^{-1}$
- $det(A^{-1})=\frac{1}{det(A)^*}$
分块矩阵
定义
将矩阵用若干条纵线和横线分成许多小矩阵,每一个小块矩阵称为子块,以子块为元素的矩阵称为分块矩阵
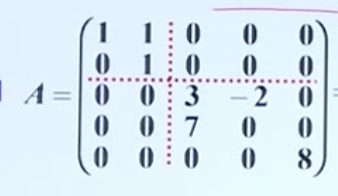
分块对角矩阵
主对角线上各子块都是方阵
分块矩阵的转置
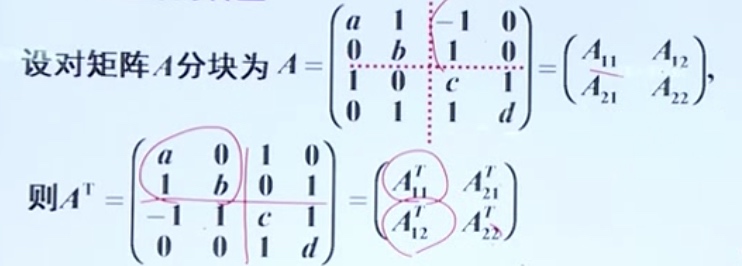
分块对角矩阵的性质
(1). 设 $A=\begin{bmatrix}A_1 &&& \ &A_2&&\&&…&\&&&A_m \end{bmatrix}$ 为分块对角矩阵,则
1). $|A|=|A_1||A_2|…|A_m|$
2). 若$|A_i|\neq 0$,则$A^{-1}=\begin{bmatrix}A_1^{-1} &&& \ &A_2^{-1}&&\&&…&\&&&A_m^{-1} \end{bmatrix}$
(2). 设有两个分块对角矩阵$A=\begin{bmatrix}A_1 &&& \ &A_2&&\&&…&\&&&A_m \end{bmatrix}$,$B=\begin{bmatrix}B_1 &&& \ &B_2&&\&&…&\&&&B_m \end{bmatrix}$
其中$A_i和B_i$为同阶方阵,则
$AB=\begin{bmatrix}A_1B_1 &&& \ &A_2B_2&&\&&…&\&&&A_mB_m \end{bmatrix}$




