
二阶行列式
行列式表示的是一个数。可以用来求解二元线性方程组。
$$
A =
\begin{vmatrix}
a_{11} & a_{12}\
a_{21} & a_{22}\
\end{vmatrix}
$$

三阶行列式

n阶行列式

余子式与代数余子式

性质
- 一个排列中的任意两个元素兑换,排列改变奇偶性
- 行列式与它的转置行列式相等
- 互换行列式的两行(列),行列式变号
- 如果行列式有两行(列)完全相同,则此行列式等于0
- 行列式的某一行(列)中的元素都乘以同一数k,等于用数k乘以此行列式
- 行列式中某一行(列)的所有元素的公因子可以提取到行列式记号外面
- 行列式中如果有两行(列)元素成比列,则此行列式等于0
- 若行列式的某一列元素都是两数之和,例如第i列的元素都是两数之和
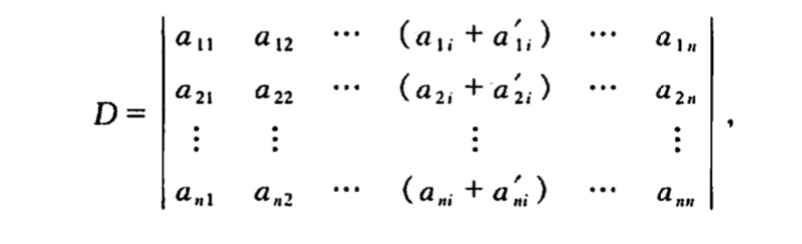
则D等于下面两个行列式之和

- 把行列式的某一行(列)的各元素乘以同一数然后加到另一列对应的元素上去,行列式不变
- 一个n阶行列式,如果其中第i行所有元素除(i,j)元 $a_{ij}$外都是零,那么这个行列式等于$a_{ij}$与它的代数余子式的乘积 $D=a_{ij}A_{ij}$
- 行列式等于它的任意一行(列)的各元素与其对应的代数余子式乘积之和
- 行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于0




